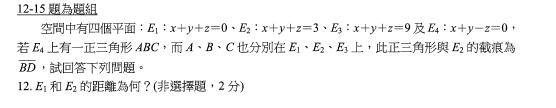112年度 全國分科 模考 數甲 試題B卷 詳解
答案:(3)在複數平面上令$A(1),B(-1)$,則$|z^2-1|=|z^2-(-1)|$表示$z^2$落在$\overline{AB}$的中垂線上,即是$y$軸上,所以實部等於$0$。設$z=a+bi$,則$z^2=a^2-b^2+2abi$。因為$z^2$的實部等於$0$、虛部小於$0$,故$a^2=b^2$且$ab<0$,則$b=-a\Rightarrow z=a-ai$。$|z-1|=|a|=|z+i|$,故$z$到$1$的距離等於$z$到$-i$的距離。#
SOL:
答案:(4)總共分割成$n^3$個小立方體,其中有$(n-2)^3$個小立方體沒有塗到顏色,故$a_n=n^3-(n-2)^3$所以$S=2^3+4^3+\cdots+198^3+200^3-(2^3+4^3+\cdots+198^3=200^3)$,故$\log S=\log200^3=3\cdot(2+\log2)\approx 6.9$。#
SOL:
答案:(5)
$\sqrt{1-\sin 8}=\sqrt{\sin^24+\cos^24-2\sin4\cos4}=\sqrt{(\sin4-\cos4)^2}=|\sin4-\cos4|$由半角公式$\cos(\frac{\theta}{2})=\pm\sqrt{\frac{1+\cos\theta}{2}}$,所以$1+\cos8=2 \cos^2 4$因為$4$弧度為第三象限角,所求等於$2\sqrt{(\sin4-\cos4)^2}+2\sqrt{\cos^24}=2|\sin4-\cos4|+2|\cos4|=-2\sin4$。#
SOL:
解答:(1)(2)(3)(5)(1)首項係數大於零,圖形開口向上,有最小值。(2)最小值發生在圖形的頂點位置,故頂點的$x$坐標為$\frac{-a}{2}=-1$,最小值為$f(-1)$。(3)當$a=2$時,範圍內的最大值發生在$x=1$,故$f(1)=1^2+2+0=3$。(4)若$f(x)=x^2-2x+3$,則在$0\leq x\leq1$時的最大值為$3$,但$a=-2$。(5)因為在$0\leq x\leq1$內最大值發生在左或右端點,故最大值為$f(0)=0或f(1)=0$,即$b=0或a+b=-1$。
SOL:
解答:(2)(5)令$a^x=b^y=c^z=t$,則$a=t^{\frac{1}{x}},b=t^{\frac{1}{y}},c=t^{\frac{1}{z}}$(1)若選項成立,則$2^3=4^2=8^1\Rightarrow 8=16=8$,矛盾。(2)$ab=t^{\frac{1}{x}}\cdot t^{\frac{1}{y}}=t^{\frac{1}{x}+\frac{1}{y}}=1$,則$\frac{1}{x}+\frac{1}{y}=0\Rightarrow y=-x$。(3)若$(a,b,c)=(\frac{1}{2},\frac{1}{4},\frac{1}{8})$,則$(x,y,z)=(1,\frac{1}{2},\frac{1}{3})$。(4)因為$ab=t^{\frac{1}{x}+\frac{1}{y}}=t^{\frac{1}{z}}$,故$\frac{1}{x}+\frac{1}{y}={\frac{1}{z}}$。(5)$abc=t^{\frac{1}{x}+\frac{1}{y}+\frac{1}{z}}=1$,則$\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=0$。
SOL:
答案:(2)(3)(5)$S$的圖形,如圖所示(1)$A$矩陣為將圖形對$x$軸對稱,因為$S$對稱於$x$軸,所以$A$矩陣的變換後會與$S$重合。(2)$A$矩陣為將$x$坐標$2$倍;$y$坐標$3$倍,所以變換後得到下圖,故$S$與$S'$不相交。(3)$A$矩陣為逆時針旋轉$270^{\circ}$,旋轉後會跟原圖形重合。(4)$A$矩陣為$135^{\circ}$鏡射矩陣,所以將圖形對$y=-x$對稱,因為$S$對稱於$y=-x$,所以$A$矩陣的變換後會與$S$重合。(5)$A$矩陣為推移矩陣,延著$x$軸方向推移$y$坐標的$-2$倍,所以變換前後如下圖重疊部份為一平行四邊形,其面積為$1\cdot2=2$。
SOL:
解答:(2)(3)(5)(1)$x=1$是甲第一次就沒投中,所以只記錄$1$次投擲。所以$P(x=1)=0.4$。(2)$x=1且y=1$表示甲沒中而且乙也沒中,所以$P(x=1組y=1)=0.4\cdot0.7=0.28$。(3)$p(x+y>3)=1-P(x+y \leq 3)=1-P(x=1且y=1)-P(x=1且y=2)-P(x=2且y=1)$$=1-0.28-0.4\cdot0.3\cdot0.7-0.6\cdot0.4\cdot0.7=1-0.28-0.084-0.168=0.468>0.45$。(4)若甲沒有中表示成功,投中表示失敗,則隨機變數為$X~G(0.4)$,則$E(x)=\frac{5}{2}$。(5)若乙沒有中表示成功,投中表示失敗,則隨機變數為$X~G(0.7)$,則$Var(Y)=\frac{0.3}{o.7^2}=\frac{30}{49}$。
SOL:
答案:(1)(2)(3)(4)(5)如圖所示,$x$軸所截的弦對應的圓心角為$frac{\pi}{2}$。因為弦長等於$2$,所以半徑$r=\sqrt{2}$。(1)圓心到$x$軸的距離為等腰直角三角形斜邊上的高,故圓心到$x$軸的距離為$\frac{\sqrt{2}}{2}r$。(2)圓心到直線$x-2y=0$的距離為$\frac{|a-2b|}{\sqrt{5}}=\frac{\sqrt{5}}{5}$,可解得$|a-2b|=1$。(3)$r=\sqrt{2}$(4)$|b|=\frac{\sqrt{2}}{2}r=1$,$b=\pm1$。代入$|a-2b|=1$,可解得$(a,b)=(1,1)、(-1,-1)、(3,1)、(-3,-1)$,與$y$軸相交的圓,圓心為$(a,b)=(1,1)或(-1,-1)$,故圓心在$y=x$上。(5)承上,符合條件的圓只有兩個。
SOL:
答案:96把問題看成$1、3、5、7、a$取三個數的排列,其中$a=6或9$,有兩個選擇。一.取到$a$$C^4_2\cdot3!\cdot2=72$二.未取到$a$$C^4_3\cdot3!=24$因此共有$72+24=96$種情況。#
SOL:
答案:4+4$\sqrt{2}$此圖形為正八邊形,所以令$D(0,0)、E(-2,0)$,則其它頂點坐標為$C(\sqrt{2},\sqrt{2})、B(\sqrt{2},2+\sqrt{2})、A(0,2+2\sqrt{2})$。$\overrightarrow{AE}=(-2,0)-(0,2+2\sqrt{2})=(-2,-2-2\sqrt{2})$且$\overrightarrow{BC}=(\sqrt{2},\sqrt{2})-(\sqrt{2},2+\sqrt{2})=(0,-2)$,故$\overrightarrow{AE} \cdot \overrightarrow{BC}=(-2,-2-2\sqrt{2}) \cdot(0,-2)=4+4\sqrt{2}$。#
SOL:
答案:$4\sqrt{6}$令$t=z^4$,則原式可整理成$t^2-7t-144=0$,可解出$z^4=t=16$或$z^4=t=-9$。當$z^4=16$,可解出$z=\pm 2$或$z=\pm 2i$,四根。當$z^4=-9$,令$z=r(\cos\theta +i\sin \theta)$,則$z^4=r^4(\cos 4\theta +i \sin 4\theta)=9(-1+0i)$,故(1)$r^4=9\Rightarrow r=\sqrt{3}$。(2)$4\theta=\pi+2k\pi \Rightarrow \theta=\frac{pi}{4}+\frac{k\pi}{2}$,$k=0,1,2,3$。所以$z^4=-9$可解出$\frac{\sqrt{6}}{2}+\frac{\sqrt{6}}{2}i$,$\frac{\sqrt{6}}{2}-\frac{\sqrt{6}}{2}i$,$-\frac{\sqrt{6}}{2}+\frac{\sqrt{6}}{2}i$,$-\frac{\sqrt{6}}{2}-\frac{\sqrt{6}}{2}i$,四根。將八個根標式在複數平面,如下圖該八邊形由八個全等三角形組成,故面積為$8\cdot \frac{2\sqrt{3}}{2}\sin(\frac{\pi}{4})=4\sqrt{6}$。#
SOL:
答案:$\sqrt{3}$$d(E_1,E_2)=\frac{|3-0|}{\sqrt{1^2+1^2=1^2}}=\sqrt{3}$。#
SOL:
答案:(5)
$d(E_2,E_3)=\frac{|3-9|}{\sqrt{1^2+1^2+1^2}}=2\sqrt{3}$,因為$\overline{AD}:\overline{DC}=d(E_1,E_2):d(E_2,E_3)=1:2$,$\overline{AB}=\overline{AD}+\overline{DC}=3a$,如下圖$\overline{BD}^2=\overline{AB}^2+\overline{AD}^2-2\overline{AB}^2\cdot\overline{AD}^2\cos 60^{\circ}=9a^2+a^2-3a^2=7a^2$,故$\overline{BD}=\sqrt{7}a$。#
SOL:
答案:$\frac{1}{3}$令$E_2、E_4$的法向量分別為$\vec{n_2}=(1,1,1)、\vec{n_4}=(1,1,-1)$,$E_2、E_4$的夾角餘弦為$\pm \cos \theta =\pm \frac{\vec{n_2}\cdot \vec{n_3}}{|\vec{n_2}|\cdot |\vec{n_3}|}=\pm \frac{1}{3}$,取正數。
SOL:
答案:$A$到直線$\overline{BD}$的距離為$\frac{3\sqrt{6}}{4}$,$\triangle ABC$的邊長為$\frac{3\sqrt{14}}{2}$在直線$\overline{BD}$取一點$M$,令從$A$到直線$\overline{BD}$的距離等於$\overline{AM}$,則$\frac{d(A,E_2)}{\overline{AM}}=\sin \theta =\sqrt{1-(\cos \theta)^2}=\sqrt{1-(\frac{1}{3})^2}=\frac{2\sqrt{2}}{3}$,則$\overline{AM}=\frac{d(A,E_2)}{\frac{2\sqrt{2}}{3}}=\frac{3\sqrt{6}}{4}$。因為$\triangle ABD=\frac{1}{2}\overline{AM}\cdot\overline{BD}=\frac{1}{2}\overline{AB}\cdot\overline{AD}\cdot \sin60^{\circ}\Rightarrow \frac{3\sqrt{6}}{4}\cdot \sqrt{7}a=3a^2\cdot\frac{\sqrt{3}}{2}\Rightarrow a=\frac{\sqrt{14}}{2}$,故$\overline{AB}=3a=\frac{3\sqrt{14}}{2}$。
SOL:
答案:(1)直角三角形$F_1F_2P$,則$\overline{OP}=\overline{OF_2}=\sqrt{225-100}=5\sqrt{5}$。#
答案:$(4\sqrt{5},-3\sqrt{5})$令$P(x,y)$,則$$\cases{\frac{x^2}{100}+\frac{y^2}{225}=1 \\ x^2+y^2=125}$$當$y^2=125-x^2$代入,可得$\frac{x^2}{100}+\frac{125-x^2}{225}=1 \Rightarrow 225x^2+12500-100x^2=22500 \Rightarrow 125x^2=10000\Rightarrow x^2=80$,故$x=\pm 4\sqrt{5}$。因為$y^2=125-x^2=45$,故$y=\pm 3\sqrt{5}$。$P$在第四象限,故$x=4\sqrt{5}$,$y=-3 \sqrt{5}$。#
答案:準線,$x=4\sqrt{5}-10$;焦距,$5-2\sqrt{5}$因為$P(4\sqrt{5},-3\sqrt{5}),F_2(0,-5\sqrt{5})$令準線$L:x=a$,因為$d(P,L)=\overline{PF_2}=10$,故$a=4\sqrt{5}-10$。焦距為$\frac{d(F_2,L)}{2}=\frac{|4\sqrt{5}-10|}{2}=5-2\sqrt{5}$。
官方試題詳解下載:112全國分科模考 B卷 數甲官方詳解