113年度 學測 數學B 試題詳解
試題下載：113學測數B試題+解答
講解影片：建設中
1月23日（二）20：00 直播講解113學測數B考題：歪歪數學YOUTUBE頻道
SOL：
第$90$百分位數的定義為$\frac{1}{210}\cdot N =\frac{90}{100}\Rightarrow N=189$，$N$為整數，所以第$90$百分位數需取第$189$位、$190$位玩家的數據平均。因為$1+2+3+\cdots +19=180<189$，而且$1+2+3+\cdots +19+20=200>190$，故第189$位、$190$位玩家的數據均為$19$。
SOL：
$1<a<10\Rightarrow\log1<\log a<\log10\Rightarrow 0<b<1\Rightarrow \log b<\log1\Rightarrow c<0$，故$c<0<b<1$。
SOL：
如圖所示，
SOL：
令$\overrightarrow{AB}=(a,b)$，其中$-1\leq a,b\leq1$，則$$|\overrightarrow{v}+\overrightarrow{AB}|=|(-2+a,3+b)|=\sqrt{(-2+a)^2+(3+b)^2}$$故當$a=-1,b=1$時，$\overrightarrow{AB}$有最大值等於$5$。
SOL：
因為$f(x-2)=f(-x-2)$，表示為$y=f(x)$的圖形右移$2$單位後會左右對稱，因此該圖形的頂點位置在$x=-2$，故$frac{-b}{2}=-2\Rightarrow b=4$。又因為$-2 \in [-3,1]$，所以最小值發生在$x=-2$，最大值發生在$x=1$。因為最大值為最小值的$4$倍，若最小值為$m$，則$y=f(x)$通過$(-2,m)、(1,4m)$，故$$\cases{(-2)^2-4\cdot 2+c=m \\ 1^2+4\cdot 1+c=4m}\Rightarrow m=3$$
SOL：
如圖所示，令$F(1,0)、D(1,2)、B(1,2)、P(0,t)$，因為
SOL：
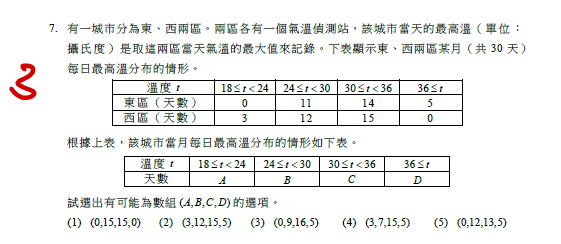
1.西區溫度$18\leq t<24$的這三天溫度必小於當天東區的溫度，故$A=0$。2.東區溫度$36\leq t$的這五天溫度必大於當天西區的溫度，故$D=5$。3.東、西二區溫度$30\leq t<36$至少有$14$天，故$C\geq14$。符合的僅$(0,9,16,5)$
SOL：
若原數列的公比為$r>0$，則(1) 為公比$-r$的等比數列(2) 為公比$\frac{1}{r}$的等比數列(3) 為公差$r$的等差數列(4) 例如：等比數列${1,2,4,8,16}$，則數列${3^1,3^2,3^4,3^8,3^{16}}$並非等比數列(5) 為公比$r^3$的等比數列
SOL：
(1) 商為$2(x^3+7x^2+x+3)$(2) 商為$x^3+7x^2+x+3$(3) $(x^3+7x^2+x+3)(x^2+5x+1)+x^2$
$=(x^3+7x^2+x+4-1)(x^2+5x+1)+x^2$
$=(x^3+7x^2+x+4)(x^2+5x+1)-5x-1$，故商為$x^3+7x^2+x+4$(4) 商為$x^3+7x^2+x+4$(5) $(x^3+7x^2+x+4)(x^2+5x+1)-x^2$
$=(x^3+7x^2+x+3+1)(x^2+5x+1)-x^2$
$=(x^3+7x^2+x+3)(x^2+5x+1)+5x+1$，故商為$x^3+7x^2+x+3$
SOL：
如圖所示，
SOL：
(1) $\frac{A-X}{X}=-0.07\Rightarrow A-X=-0.07X\Rightarrow A=0.93X$(2) $Y=0.95^4X\approx0.8145X>0.8X$(3) 成長率應以幾何平均計算之，選項(4)、(5)即為幾何平均的定義。
SOL：
該題需先了解，在$A,B,C,D$上，有$\frac{1}{2}$的機率會在原地，各有$\frac{1}{4}$的機率會往相鄰的格子前進。(1) $A到B$只有一個往右的方向，故機率為$b_1=\frac{1}{4}$(2) $b_2$有兩種情況，其一為再$A$格停留原地再到B格，另一個為先到B格再停留原地，故$b_2=\frac{1}{2}\cdot\frac{1}{4}+\frac{1}{4}\cdot\frac{1}{2}=\frac{1}{4}$(3) 走到$B$與走到$C$對稱，所以機率相同，所以$a_2+d_2=1-b_2-c_2=\frac{1}{2}$(4) 同上，所以$b_{99}=c_{99}$(5) 在$A、D$格時有一半的機率停留原地，有一半機率離開去往$B、C$格。同理，在$B、C$格時有一半的機率會離開回到$A、D$格，所以每次都有一半的機率在$A、D$格，故$a_{100}+d_{100}=\frac{1}{2}$
SOL：
$\begin{bmatrix} 1 & -1 \\ 3 & -2 \end{bmatrix} \begin{bmatrix} 2a+1 \\ 2b+1 \end{bmatrix} =\begin{bmatrix} 1 & -1 \\ 3 & -2 \end{bmatrix}\begin{bmatrix} 2a \\ 2b \end{bmatrix}+ \begin{bmatrix} 1 & -1 \\ 3 & -2 \end{bmatrix}\begin{bmatrix} 1 \\ 1 \end{bmatrix}$$= 2\begin{bmatrix} 1 & -1 \\ 3 & -2 \end{bmatrix}\begin{bmatrix} a \\ b \end{bmatrix}+ \begin{bmatrix} 1 & -1 \\ 3 & -2 \end{bmatrix}\begin{bmatrix} 1 \\ 1 \end{bmatrix}=2\begin{bmatrix} 1 \\ 0 \end{bmatrix}+\begin{bmatrix} 0 \\ 1 \end{bmatrix}=\begin{bmatrix} 2 \\ 1 \end{bmatrix}$，故$c-3d=-1$
SOL：
假設報考數$A$的學生佔全體高三學生的比例為$X$，因為報考數$A$的學生中有$\frac{5}{8}$也報考數$B$，所以全體數$A$的考生有$\frac{3}{8}$是只有報考數$A$，故只報名數$A$的考生佔全高三生的比例為$\frac{3}{8}X=\frac{3}{10}$，所以$X=\frac{8}{10}$。因此，全體高三生比例為$1$，其中$\frac{3}{10}$為只報名數$A$，而$\frac{8}{10}-\frac{3}{10}=\frac{5}{10}$為$A、B$都報名，$1-\frac{8}{10}=\frac{2}{10}$為只報名數$B$，所以只報名數$B$佔了報名數$B$的學生的比例為$$\frac{\frac{2}{10}}{\frac{2}{10}+\frac{5}{10}}=\frac{2}{7}$$
SOL：
$\overrightarrow{Q_1Q_2}=\overrightarrow{RQ_2}-\overrightarrow{RQ_1}=(\overrightarrow{P_2Q_2}-\overrightarrow{P_2R})-(\overrightarrow{P_1Q_1}-\overrightarrow{RP_1})=(\overrightarrow{P_2Q_2}-7\overrightarrow{P_2Q_2})-(\overrightarrow{P_1Q_1}-4\overrightarrow{P_1Q_1})=3\overrightarrow{P_1Q_1}-6\overrightarrow{P_2Q_2}$
SOL：
如圖所示，
SOL：
如圖所示，
SOL：
六個面+切掉八個角=十四面體
SOL：
因為$\triangle BCD$的三邊長為$9、9、8$，由海龍公式$s=\frac{9+9+8}{2}=13$，面積則等於$$\sqrt{s(s-8)(s-9)(s-9)}=\sqrt{13\cdot5\cdot4\cdot4}=4\sqrt{65}$$
沒有留言:
張貼留言