112年度 全國公私立分科 模考 數甲(B卷) 試題 詳解
SOL:
答案:(2)$a=\log_{\frac{1}{3}}^{\frac{1}{2}}<0$$b=\log_{\frac{1}{2}}^{\frac{1}{3}}=\log_2^3<\log_2^4=2$$c=5^{\frac{1}{2}}>4^{\frac{1}{2}}=2$$d=(\frac{1}{2})^5<1$故$c>2>b>1>d>0>1$
SOL:
答案:(5)因為$\frac{1}{3}\vec c =\frac{1}{3}(3\vec a+ 2\vec b)=\vec a+\frac{2}{3}\vec b$,故$\vec c 平行 (\vec a+\frac{2}{3}\vec b) $。
SOL:
答案:(4)。三角形的位置圖如下所示,直線要與之有共三交點,上下兩三角形交點數為$(1,2)或(2,1)$。
1.若交點為點$A$,則$m_{AD}=8$,$m_{AF}=-1$,故$m>8或m<-1$。2.若交點為點$B$,不會有三交點。3.若交點為點$C$,則$m_{CD}=2$,$m_{CF}=-3$,故$m>2或m<-3$。4.若交點為點$D$,則$m_{DA}=8$,$m_{DC}=2$,故$2<m<8$。5.若交點為點$E$,不會有三交點。6.若交點為點$F$,則$m_{FC}=-3$,$m_{FA}=-1$,故$-3<m<-1$。
故取聯集後最大範圍為$m>2或m<-1$。
SOL:
答案:(3)(4)(5)
SOL:
答案:(1)(2)(3)
SOL:
答案:(1)(2)(3)(4)
SOL:
答案:(3)(4)
SOL:
答案:(2)(5)
SOL:
答案:$2\sqrt{3}:3+\pi$
SOL:
答案:$38640$
【點擊下方連結觀看講解影片】
SOL:
答案:$21$
取一球的期望值等於$1\cdot\frac{1}{55}+2\cdot\frac{2}{55}+3\cdot\frac{3}{55}+\cdots+10\cdot\frac{10}{55}=\frac{1^2+2^2+\cdots+10^2}{55}=7$。故取三球的期望值等於$7\cdot3=21$。#
【點擊下方連結觀看相關觀念講解影片】
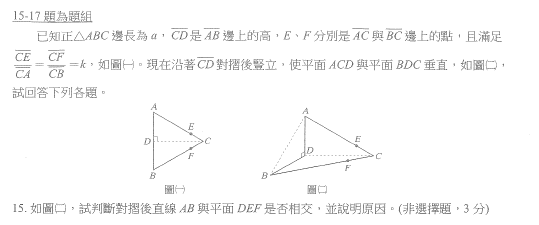
兩平面一定不會平行,所以必相交於一直線。#
$\cases{ 5y-z=-1-3t \\ -y+4z=11-t }\Rightarrow \cases{ 20y-4z=-4-12t \\ -y+4z=11-t }$,兩式相加算得$y=\frac{7}{19}-\frac{13}{19}t$,且$z=\frac{54}{19}-\frac{8}{19}t$故$L:\cases{x=t \\ y=\frac{7}{19}-\frac{13}{19}t ,t\in \mathbb{R}\\ z=\frac{54}{19}-\frac{8}{19}t} $#
$L:\cases{x=t \\ y=\frac{7}{19}-\frac{13}{19}t ,t\in \mathbb{R}\\ z=\frac{54}{19}-\frac{8}{19}t} $
代入$E_3:x+7y+az+23=0$,可算得$(72+8a)t-486-54a=0$,任何實數$t$等號均成立,所以$a=-9$。#
代入$E_4:bx+20y-23z+58=0$,可算得$(19b-76)t=0$,等號不能對任何實$t$都成立,所以$b\neq4$。#
正焦弦長等於$\frac{2b^2}{a}=\frac{6}{2}=3$。#
SOL:
$\triangle QF_1F_2的周長=(\overline{QF_1}+\overline{QF_2})+\overline{F_1F_2}=2a+2\sqrt{a^2-b^2}=2a+2\sqrt{a^2-a}$。
其中,$a^2-a>0$,故$a>1$。#
SOL:
【點擊下方連結觀看講解影片】
官方試題詳解下載:112 全模(南一)分科 模考 數甲(B卷) 官方詳解